Familien und Mengenfamilien
In der Mathematik ist eine Familie eine „Sammlung“ von Elementen, bei der dasselbe Element – im Gegensatz zu einer Menge – auch mehrfach vorkommen kann. Eine Familie wird geschrieben als
(ai)i∈I
I wird Indexmenge der Familie genannt. Wenn I eine geordnete Menge ist, dann ist auch die Familie geordnet. Das ist dann ebenfalls ein Unterschied zu einer Menge, wo die Elemente im Allgemeinen keine bestimmte Reihenfolge haben.
Beispiele
| Indexmenge | ergibt | genannt | Vorteil | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I = {1, 2} | (a1, a2) | geordnetes Paar | „Familie“ ist Oberbegriff – man muss sich nicht festlegen, wie „groß“ (mächtig) I ist. | ||||||||||||||
| I = {1, ..., n} | (a1, ..., an) | n- | |||||||||||||||
| I = ℕ | (ai)i∈ℕ
| Folge
| I = ℝ
| (ai)i∈ℝ
| Funktion
| I = {1, ..., n} × {1, ..., m}
| 
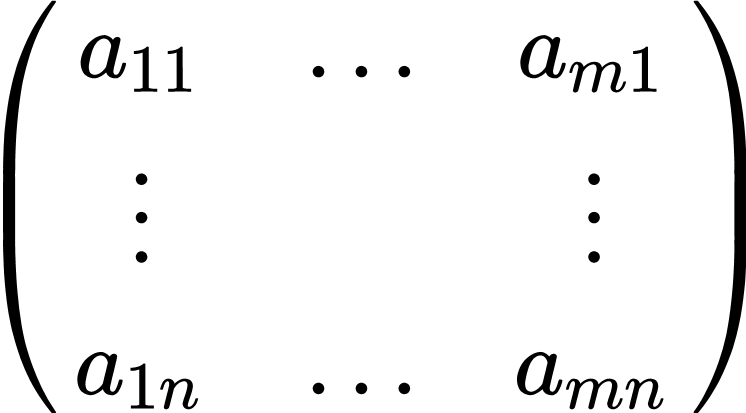
(n × m)- | So lassen sich lineare Abbildungen zwischen Vektorräumen kompakt und übersichtlich angeben. (Man spricht bei den Einträgen in einer Matrix selten von einer Familie, aber ohne dem Begriff Familie lässt sich der Begriff Matrix schwer definieren.)
| I = Familie (ij)j∈J
| (aij)j∈J
| Zusammensetzung von Familien
| Z. B. zur Auswahl bestimmter Mitglieder aus einer Familie, woraus eine neue Familie entsteht
| I = die zu beschreibende Familie A
| A = (a)a∈A
| (D. h. die „Familienmitglieder“ sind die Elemente der Menge A und werden durch sich selbst indiziert. Es kann in dem Fall daher keine 2 gleichen „Familienmitglieder“ geben.) Menge (Wird auch wie eine Menge – ohne Klammern und ohne Indexmenge – geschrieben.)
| „Familie von Mengen“ ist einfacher als „Menge von Mengen“, wo man die verschiedenen Arten von Mengen verwechseln könnte. Insbesondere kann man ohne viele Worte „Familienmitglieder“ von sonstigen Mengen unterscheiden. Hilft somit, nicht durcheinanderzukommen.
| |
Definition
| Sonderfälle | |
|---|---|
| Eine Familie ist eine Funktion von einer Menge I in eine Menge A. |
|
| Die Menge aller Familien von Elementen aus A mit Indexmenge I | |||||
| = | das kartesische Produkt von A, |I|-| =
| die Menge aller Funktionen von I nach A
| =
| AI
| |
Verwendung
Obwohl Familien im Grunde dasselbe wie Funktionen oder kartesische Produkte sind, betrachtet man sie in der Praxis meist nur als „Sammlung“ von Elementen.[1]
D. h. die „Zusammenfassung“ von nicht notwendigerweise verschiedenen Elementen kann man als den eigentlichen Zweck von Familien betrachten, und die Funktionen als hierfür nötigen Unterbau.
Fehler
- Manchmal werden Familien als {ai}i∈I abgekürzt, aber geschwungene Klammern sollten für Mengen reserviert sein.
Oftmals wird fälschlicherweise von einer Menge gesprochen, wenn eine Familie gemeint und erforderlich ist. Würde man etwa in der Theorie der Vektorräume den Begriff lineare Unabhängigkeit für Mengen statt Familien von Vektoren definieren, könnte man noch nicht einmal formulieren, dass zwei vom Nullvektor verschiedene Vektoren u. a. dann linear abhängig sind, wenn sie gleich sind. In dem Fall würden sie zusammen nämlich nur eine einelementige Menge bilden, die dann linear unabhängig ist.
Weiter
| Mengen von Mengen – Werden oft auch als Familien bezeichnet, selbst wenn es keine Indexmenge gibt. |
Weblinks
- Wikipedia, Artikel Multimenge – Wäre eine Alternative zu Familien, wird aber eher nur für Computer (in der Informatik) verwendet, und dasselbe Element darf hier meist nicht unendlich oft vorkommen. Manche mathematischen Sätze könnten einfacher mit Multimengen geschrieben werden, aber Operationen mit Multimengen sind komplizierter.
Quellen
| [1] | englische Wikipedia, Artikel „Indexed family“, Abschnitt „Formal definition“ – „In practice ..., a family is viewed as a collection, rather than a function.“ |