Operationen mit Mengen
Was man mit allen Mengen tun kann:
Mit einer Menge
| Operation | Abk. | Beispiel | gesprochen | Beschreibung | formale Bedingung |
|---|---|---|---|---|---|
| |...| | |A| | Kardinalität von A | Anzahl der Elemente (bei endlicher Menge) bzw. „Stufe“ der Unendlichkeit | |
| 𝒫 | 𝒫(A) | Potenzmenge von A | Menge aller Teilmengen | X ⊆ A | |
| [...] oder 𝒫 mit Index | [A]2 | Menge aller 2-elementigen Teilmengen von A | X ⊆ A ∧ |X| = 2 | |
| 𝒫2(A) | |||||
| [A]<ω | Menge aller endlichen Teilmengen von A | X ⊆ A ∧ |X| < ω | |||
| 𝒫fin(A) | |||||
| [A]ω | Menge aller abzählbar unendlichen Teilmengen von A | X ⊆ A ∧ |X| = ω | |||
| 𝒫ω(A) | |||||
| [A]≤ω | Menge aller höchstens abzählbar unendlichen Teilmengen von A | X ⊆ A ∧ |X| ≤ ω | |||
| 𝒫≤ω(A) | |||||
| TC | TC(A) | transitive Hülle von A | Für alle Elemente von A (die wieder Mengen sind) werden deren Elemente direkt zu A hinzugefügt. Das wird so lange wiederholt, bis keine neuen Elemente hinzuzufügen sind. | y ∈ x ∧ x ∈ A ⇒ y ∈ A |
Mit 2 Mengen
Das sind die Mengenoperationen im engeren Sinn:
| Operation | Abk. | Beispiel | gesprochen | Beschreibung | formale Bedingung | grafisch |
|---|---|---|---|---|---|---|
| ∪ | A ∪ B | A vereinigt (mit) B | Elemente, die in mindestens einer der beiden Mengen (A oder B) vorkommen | x ∈ A ∨ x ∈ B | 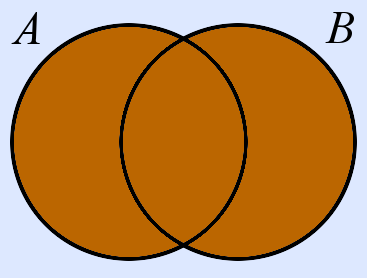
|
| ∩ | A ∩ B | A geschnitten (mit) B | Elemente, die in beiden Mengen (A und B) vorkommen | x ∈ A ∧ x ∈ B | 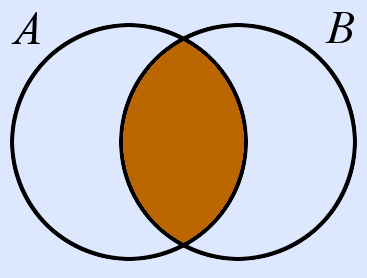
|
| \ | A \ B | A ohne B | Elemente, die in der ersten, aber nicht in der zweiten Menge vorkommen | x ∈ A ∧ x ∉ B | 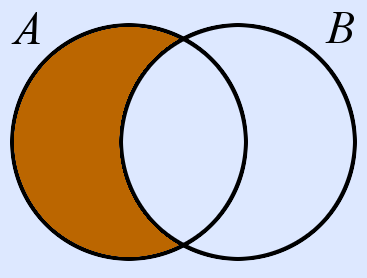
|
| △ | A △ B | symmetrische Differenz von A und B | Elemente, die entweder in der Menge A oder in der Menge B vorkommen (aber nicht in beiden) | x ∈ A ∪ B ∧ x ∉ A ∩ B | 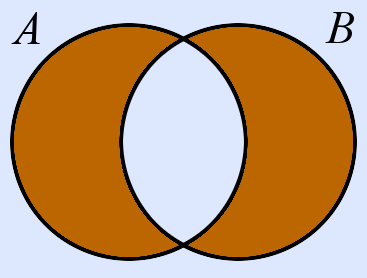
|
| C | AC | A Komplement | Elemente einer fixen, separat gegebenen Grundmenge G, die nicht in A vorkommen (AC ist also nur eine Kurzschreibweise für G \ A.) | x ∈ G ∧ x ∉ A | 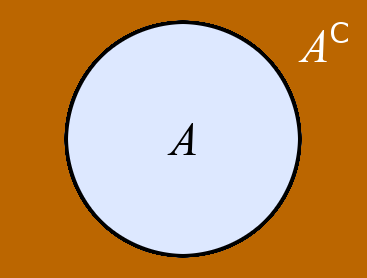
|
| ’ | A’ | |||||
| × | A×B | A mal B | Menge der geordneten Paare | (a, b) mit a ∈ A ∧ b ∈ B | 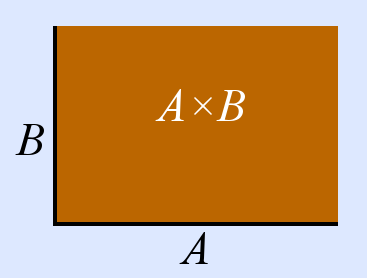
|
Mit beliebig vielen Mengen
Die folgenden Operationen sind auch für beliebig viele (sogar überabzählbar viele) Mengen möglich:
| Operation | Schreibweise | alternativ (𝒜 = Menge aller Ai) | ergibt für leere Indexmenge (Sonderfall) | |||
|---|---|---|---|---|---|---|
|
| ⋃ 𝒜 | ∅ | |||
|
| ⋂ 𝒜 | Grundmenge (wenn vorhanden, sonst nicht definiert) | |||
|
| ∏ 𝒜 | {∅} | |||
| = Menge aller Funktionen, die jedem i ∈ I ein Element aus Ai zuordnen | ||||||
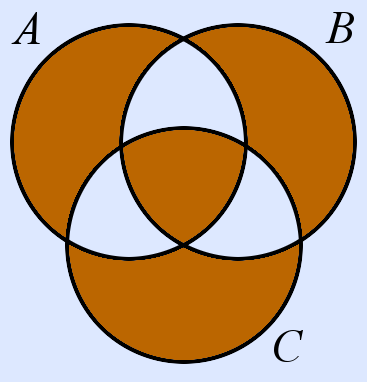
(A △ B) △ C
Differenz und symmetrische Differenz werden nur selten für mehr als 2 Mengen betrachtet. Die symmetrische Differenz von 3 oder mehr Mengen liefert alle Elemente, die in einer ungeraden Anzahl von Mengen enthalten sind (siehe Beispiel rechts). Für unendlich viele Mengen ist daher keine symmetrische Differenz definiert.