Mengen

Mengen sind der Grundbegriff der modernen Mathematik. Mit ihnen kann man Zahlen oder beliebige andere mathematische Objekte zu einem Ganzen zusammenfassen.

Zeichen, Begriffe und Beispiele

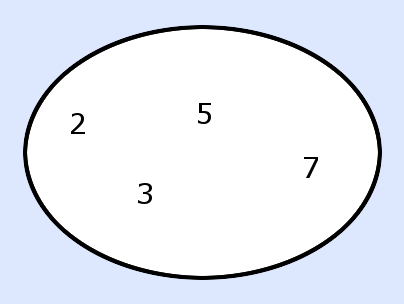
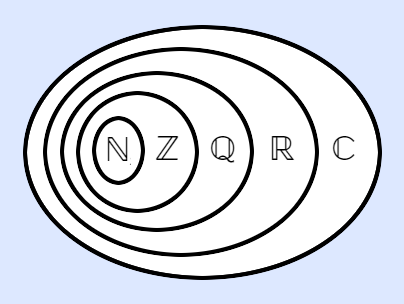
So werden Mengen oft grafisch dargestellt (Venn-Diagramm).

Veranschaulichung der Teilmengenbeziehung der gängigen Zahlenbereiche (Beachte, dass hier – im Gegensatz zum ersten Diagramm – die Namen der Mengen und nicht ihre Elemente eingetragen sind.)

Zeichen	Bedeutung	Beispiel/Erläuterung
{ ... }	Mengenklammern (zur Definition einer Menge)	{2, 3, 5, 7}	Menge aller Primzahlen kleiner als 10 (Die Zahlen 2, 3, 5 und 7 sind die Elemente dieser Menge.)
{ ... }	Mengenklammern (zur Definition einer Menge)	{12, 24, 36, 48, 60, ...}	alle Vielfachen von 12 (unendliche Menge)
∅	leere Menge		∅ ist an der Hochschule gebräuchlich; {} in der Schulmathematik.
{}	leere Menge
∈	Element von	`x` ∈ ℝ	`x` ist ein Element der Menge der reellen Zahlen. = `x` ist eine reelle Zahl.
∋	enthält	ℝ ∋ π	Die Menge der reellen Zahlen enthält die Zahl π.
∉	kein Element von	√2 ∉ ℚ	√2 ist kein Element der Menge der rationalen Zahlen. = √2 ist keine rationale Zahl.
\|	für die gilt / mit der Eigenschaft	{`x` ∈ ℝ \| `x`² ∈ ℤ}	Menge aller reellen Zahlen, für die das Quadrat eine ganze Zahl ist = alle Quadratwurzeln ganzer Zahlen (≥ 0)
:	für die gilt / mit der Eigenschaft	{`x` ∈ ℝ \| `x`² ∈ ℤ}
⊆	ist eine Teilmenge von	ℕ ⊆ ℝ	Die Menge der natürlichen Zahlen ist eine Teilmenge der Menge der reellen Zahlen.
⊂	ist eine *echte* Teilmenge von	`A` ⊂ `B`	`A` ist eine Teilmenge von `B`, aber nicht gleich `B` (sondern eine kleinere Menge).
⊊	ist eine *echte* Teilmenge von		Das Zeichen ⊊ brauchen nur Autoren, die ⊂ auch für unechte Teilmengen verwenden (weil sie selten nur über echte Teilmengen sprechen müssen).
⊇	analog für Obermengen	ℝ ⊇ ℕ	Die Menge der reellen Zahlen ist eine Obermenge der Menge der natürlichen Zahlen.
⊃
⊋

Definition

Was eine Menge ist, wird heutzutage durch gewisse Grundannahmen (Axiome) definiert. Ein rein intuitiver Zugang („naive Mengenlehre“) hat sich nicht bewährt: Dabei ist man auf Widersprüche gestoßen.

Z. B. ist es nicht möglich, von der „Menge aller Mengen“ zu sprechen. Stattdessen sollen Mengen ausschließlich aus bereits definierten Mengen gebildet werden.

Insbesondere würde ich als Elemente nur mathematische Objekte zulassen. In einführenden Texten ist oft die Rede von „Mengen von Schülern“ oder dgl., aber das sind keine Mengen im präzisen mathematischen Sinn. Was wäre z. B. in der Menge aller pünktlichen Züge enthalten? Ist eine U-Bahn ein Zug? Ist eine Verspätung von 1 Minute noch „pünktlich“? In der reinen Mathematik werden solche Fragen nicht gestellt. Braucht man auch nicht, denn Schülern, Zügen etc. kann man je eine Zahl zuordnen und hat dann – wenn die Zugehörigkeit geklärt ist – eine mathematische Menge mit den gleichen Eigenschaften. (Nur die Bezeichnung ihrer Elemente ist anders, und auf Bezeichnungen kommt es, rein logisch betrachtet, nie an.)

Eigenschaften

		Beispiel
Die Elemente einer Menge haben keine bestimmte Reihenfolge (obwohl man sie u. U. in einer gewissen Reihenfolge aufschreibt).		{1, 2, 3} = {3, 1, 2}
Mengen können nicht dasselbe Element zweimal enthalten.		Fügt man zur Menge aller geraden Zahlen {2, 4, 6, 8, ...} alle Vielfachen von 3 (also 3, 6, 9, ...) hinzu, erhält man {2, 3, 4, 6, 8, 9, ...}. Die Zahl 6 und ihre Vielfachen sind nachher nicht doppelt in der Menge vertreten.
Elemente können auch Mengen sein.		{∅, {0}, {1}, {0, 1}} = Menge aller Teilmengen von {0, 1}
Aber Mengen dürfen nicht sich selbst als Element enthalten.	(Fundierungs- axiom)	`A` ∈ `A`
Mengen dürfen sich auch nicht gegenseitig als Element enthalten (weder unmittelbar noch über „dazwischengeschaltete“ Mengen).		`A` ∈ `B` und `B` ∈ `A` `A`₁ ∈ `A`₂ ∈ ... ∈ `A_n` ∈ `A`₁
Mengen dürfen nicht eine Menge enthalten, die wieder eine Menge enthält und die wieder eine usw. ohne Ende. (D. h. es ist keine unendlich absteigende Kette erlaubt.)		`A`₁ ∋ `A`₂ ∋ `A`₃ ∋ ... Z. B.: `A`₁ = {`A`₂} `A`₂ = {`A`₃} `A`₃ = {`A`₄} ...
Unendlich aufsteigende Ketten sind erlaubt.		`A`₂ = {`A`₁} `A`₃ = {`A`₂} `A`₄ = {`A`₃} ...

Kritik

Nur noch selten stößt man auf Einwände wie die folgenden:

	Meine Meinung
Manchmal wird noch kritisiert, dass eine Menge keine scharfe Definition hätte („Was ist, wenn eine Katze eine Menge von Socken frisst? Wo ist dann die Menge?“).	kein berechtigter Einwand bei Mengen von mathematischen Objekten
Die Grundannahmen (Axiome) über Mengen halten manche für nicht einleuchtend, und innere Widersprüche lassen sich nicht zweifelsfrei ausschließen.^[1]	Es wird jetzt schon lange mit der Mengenlehre gearbeitet, und es sind keine Widersprüche aufgetreten. Ein Grundbegriff hängt immer zu einem gewissen Grad „in der Luft“.
Kritik an unendlichen Mengen	Rein philosophische Kritik – Weder in der Theorie noch in der Praxis gibt es Probleme mit unendlichen Mengen.
Kritik an der Mengenlehre im Schulunterricht	Ja, ist vielleicht wirklich manchmal übertrieben.

Vergangenheit

Mengen im heutigen Sinn wurden Ende des 19. Jahrhunderts von Georg Cantor in die Mathematik eingeführt. Auslöser war, dass er untersuchte, für welche reellen Zahlen eine Funktion nicht durch eine bestimmte unendliche Summe von einfacheren Funktionen (Fourierentwicklung) angenähert werden kann. Da begann er, beliebige Teilmengen von ℝ zu betrachten.^[2]

Weiter

Operationen mit Mengen

Siehe auch

Kardinalzahlen – Geben die Zahl der Elemente einer (endlichen oder unendlichen) Menge an.

Weblinks

Oliver Deiser: Einführung in die Mengenlehre – ausführliches Online-Buch
Achim Blumensath: Set Theory (PDF) – gut motivierte Einführung (zumindest am Anfang)
Stefan Geschke: Einführung in die Mengenlehre (PDF)
Wikipedia, Artikel Von-Neumann-Hierarchie – zur Konstruktion von (nahezu) beliebig großen Mengen
Stanford Encyclopedia of Philosophy, Artikel The Early Development of Set Theory – über die Anfänge und die Schwierigkeiten dabei

Quellen

[1]

Rudolf Taschner: Lehrgang der konstruktiven Mathematik. 1. Teil: Zahl und Kontinuum. Wien: Manz, 1991, S. 214 – „Alle bis jetzt ... [für Mengen] entwickelten Axiomensysteme sind ... außerordentlich unanschaulich, widersprechen sogar der intuitiven Vorstellung von Mengen und für keines der bis jetzt ersonnenen Axiomensysteme besteht auch nur die geringste Hoffnung, dass man zweifelsfrei nachweisen kann, ob mit ihm tatsächlich alle inneren Widersprüche aus der Theorie verbannt wären.“

[2]

Thomas Streicher: Einführung in die Axiomatische Mengenlehre (PDF), S. 2 – „die Menge aller reellen Zahlen, für die die Fourierentwicklung einer Funktion f entweder nicht konvergiert oder mit dem Wert von f nicht übereinstimmt[,] ... war für Georg Cantor, den Begründer der Mengenlehre, der Auslöser, beliebige Teilmengen von ℝ zu betrachten.“
Jörg Resag: Die Grenzen der Berechenbarkeit, Abschnitt Die Mächtigkeit unendlicher Mengen – „Die Idee, Begriffe wie die Menge der Ausnahmepunkte oder die Menge der Häufungspunkte der Menge der Ausnahmepunkte zu verwenden, war geboren.“

Seite erstellt am 27.11.2024 – letzte Änderung am 8.12.2024

Mathematik

Wissenschaft

Hauptthemen

Neue und erweiterte Seiten