Primzahlen
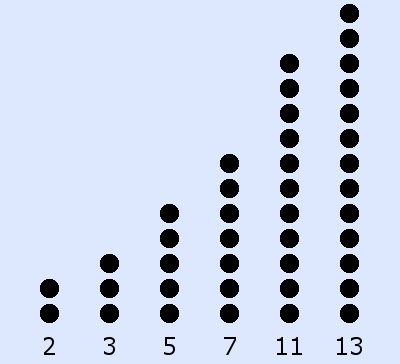
Keine Anordnung als Rechteck möglich
Keine Primzahlen
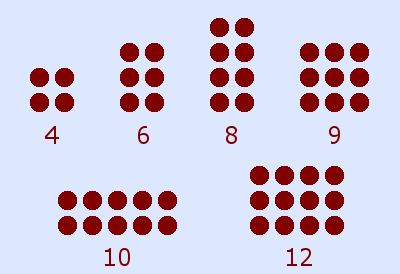
Anordnung als Rechteck möglich
Primzahlen
Eine Primzahl ist eine natürliche Zahl, die größer als 1 ist und nur durch 1 und sich selbst ohne Rest geteilt werden kann. Die kleinsten Primzahlen sind:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...
Primzahlen sind faszinierend, denn
bis heute [ist] kein einfaches Muster unter der Folge ... der Primzahlen entdeckt worden. Zum Beispiel gibt es kein „schnelles“ Verfahren, die n-te Primzahl zu berechnen. Die genaue Natur der Primzahlen ist bis heute ein bedeutendes offenes Problem.
Sie wachsen wie Unkraut unter den natürlichen Zahlen, scheinbar keinem anderen Gesetz als dem Zufall unterworfen, und kein Mensch kann voraussagen, wo wieder eine sprießen wird, noch einer Zahl ansehen, ob sie prim ist oder nicht.
Ich stell mir eine Primzahl als eine Anzahl von Punkten vor, die sich nicht zu einem Rechteck anordnen lassen (siehe Bilder). Erstaunlich ist,
- dass bei immer größeren Zahlen immer neue „Lücken“ aufscheinen, wo sich eine Zahl befindet, die kein Vielfaches einer kleineren Zahl ist – Es gibt einfach nicht „genug“ mögliche Rechtecke.
- dass die Folge der Primzahlen so unregelmäßig erscheint – Primzahlen „gehören zu den willkürlichsten, widerspenstigsten Objekten, die der Mathematiker überhaupt studiert.“
- dass man trotz der scheinbar zufälligen Folge etwas über die Anzahl und Verteilung von Primzahlen sagen kann (zumindest gute Schätzwerte)
Bedeutung in der Mathematik
Primzahlen sind wichtiger als ich ursprünglich dachte, vor allem weil sich jede natürliche Zahl (außer 0) eindeutig als Produkt von Primzahlen darstellen lässt (Primfaktorzerlegung, Hauptsatz der Arithmetik). – Das ist übrigens einer der Gründe, warum man die Zahl 1 nicht zu den Primzahlen zählt, denn wenn man 1 dazumultiplizieren kann oder auch nicht, wäre die Zerlegung nicht mehr eindeutig.
Außerdem hängen Primzahlen eng mit der Riemannschen Zetafunktion zusammen – eine Funktion von einer komplexen Zahl auf eine andere komplexe Zahl, in die alle Primzahlen „hineincodiert“ sind. Beispiel: Wenn die Verteilung von Primzahlen „zufällig“ ist, dann hat die Zetafunktion ganz bestimmte Nullstellen (Riemannsche Vermutung).
Anwendung
Große Primzahlen werden zur Verschlüsselung verwendet (z. B. von Webseiten). Das funktioniert, weil man z. B. eine hundertstellige Zahl praktisch nicht in ihre Primfaktoren zerlegen kann. Es gibt dafür kein schnelles Verfahren (zumindest bis jetzt).
Bezeichnung
Primzahl soll primäre (lateinisch: erste) Zahl bedeuten, womit offenbar gemeint ist, dass bei diesen die Vielfachen einer nicht weiter teilbaren Zahl „starten“.
Statt „... ist Primzahl“ sagt man auch „... ist prim“.
Weiter
Weblinks
- The PrimePages: prime number research & records (englisch)
- Oliver Deiser: Die Unendlichkeit der Primzahlen (kostenloses Online-
Buch)