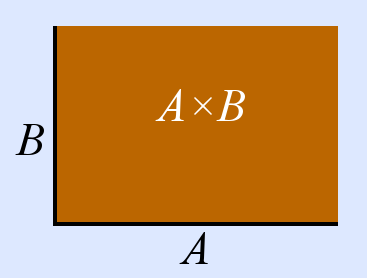
Beim Begriff „kartesisches Produkt“ denkst du vielleicht an ein kartesisches Koordinatensystem, und das ist gar nicht verkehrt. Das kartesische Produkt ist eine Art Verallgemeinerung von kartesischen Koordinatensystemen:
|
| formal
|
| Abk.
| Sonderfall wenn alle Mengen gleich sind
|
- Das kartesische Produkt von 2 Mengen sind alle geordneten Paare von Elementen aus der ersten bzw. zweiten Menge.
| {(a, b) | a ∈ A ∧ b ∈ B}
| =
| A × B
| A2
|
- von 3 Mengen sind es alle Tripel
|
| {(a, b, c) |
| a ∈ A ∧
| | b ∈ B ∧
| | c ∈ C}
|
| =
| A × B × C
| A3
|
- von 4 Mengen sind es alle Quadrupel
|
| {(a, b, c, d) |
| a ∈ A ∧
| | b ∈ B ∧
| | c ∈ C ∧
| | d ∈ D}
|
| =
| A × B × C × D
| A4
|
- von n Mengen sind es alle n-Tupel
|
| {(a1, ..., an) |
| a1 ∈ A1 ∧
| | ... ∧
| | an ∈ An}
|
| =
| A1 × ... × An
| An
|
| =
|
|
- für abzählbar unendlich viele Mengen sind es alle unendlichen Folgen
|
| {(an)n∈ℕ |
| ai ∈ Ai ∀i ∈ ℕ}
|
| =
|
| Aℕ
|
- für beliebig viele Mengen, gegeben als Mengenfamilie (Ai)i∈I, sind es alle Funktionen, die jedem i ∈ I ein Element aus Ai zuordnen
(Diese Definition gilt tatsächlich auch für endlich viele Mengen, da z. B. ein geordnetes Paar nichts anderes als eine Funktion ist, die 1 auf a und 2 auf b abbildet.)
| {Funktionen f : I → ⋃i∈I Ai | f(i) ∈ Ai ∀i ∈ I}
| =
|
| AI
(Das ist die übliche Schreibweise für die Menge aller Funktionen von I nach A, und das gilt sogar für alle Einträge in dieser Spalte, da z. B. 2 mengentheoretisch gleich {0, 1} ist, weshalb A2 = A{0, 1} = Menge aller Funktionen von {0, 1} nach A ist. Sehr elegant!)
|