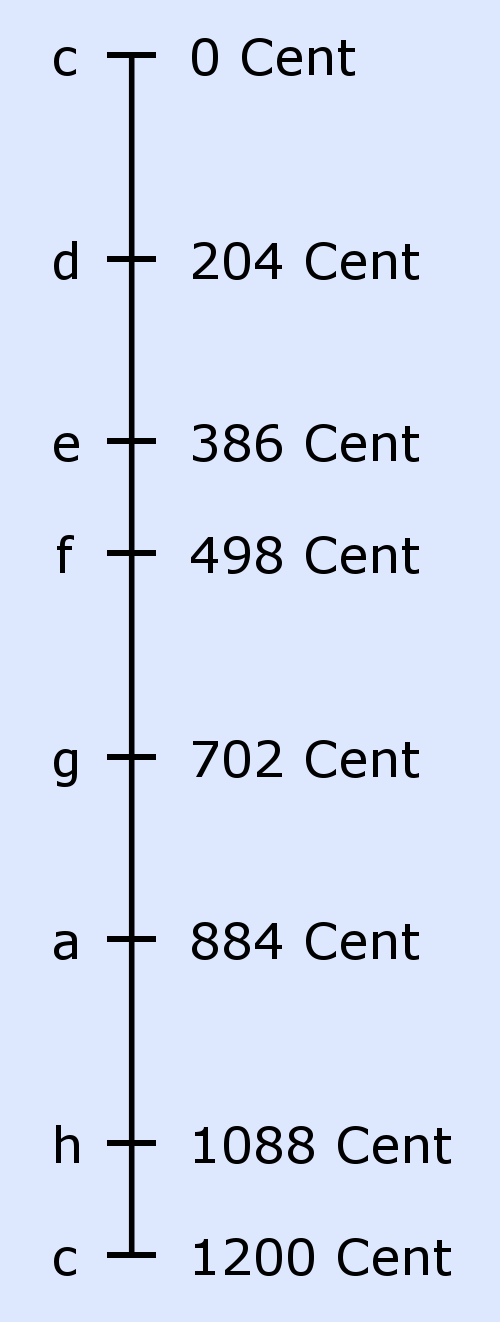
Die Tonleiter auf der Cent-
Definition und Schreibweise der gängigen Tonleiter
In der Musik werden bestimmte wohlklingende Frequenzverhältnisse verwendet. Die in westlichen Ländern benutzte Auswahl basiert auf folgenden Stammtönen:
| Abk. | Name des Frequenzverhältnisses | Frequenz | |||
|---|---|---|---|---|---|
| c | Prime (Grundton) | 0 Cent | |||
| d | Sekunde | 1/8 höher als Grundton | ≈ 204 Cent | 1/8 höher als voriger | ≈ 204 Cent |
| e | große Terz | 1/4 höher als Grundton | ≈ 386 Cent | 1/9 höher als voriger | ≈ 182 Cent |
| f | Quarte | 1/3 höher als Grundton | ≈ 498 Cent | 1/15 höher als voriger | ≈ 112 Cent |
| g | Quinte | 1/2 höher als Grundton | ≈ 702 Cent | 1/8 höher als voriger | ≈ 204 Cent |
| a | große Sexte | 2/3 höher als Grundton | ≈ 884 Cent | 1/9 höher als voriger | ≈ 182 Cent |
| h | große Septime | 7/8 höher als Grundton | ≈ 1088 Cent | 1/8 höher als voriger | ≈ 204 Cent |
| c | Oktave | 2-| = 1200 Cent
| 1/15 höher als voriger
| ≈ 112 Cent
| |

Quelle (verändert): Patrick-
Tonleiter in der Notenschrift – Hier sind die ungleichmäßigen Abstände nicht erkennbar.
Diese Tonleiter heißt C-Dur und entspricht den weißen Tasten eines Klaviers. Sie enthält die wichtigsten Harmonien (= kleine Zähler und Nenner in den Bruchzahlen), die man ausgehend von einem Ton spielen kann. Nach erfolgter Frequenzverdopplung (letzte Zeile) wiederholt sich die Tonleiter. Daher ist der letzte Ton in obiger Tabelle wieder ein c (= Grundton für die folgenden Töne).
Schwarze Klaviertasten
In der Tonleiter ist zwischen e und f sowie zwischen h und c ein geringerer Abstand als zwischen den anderen Tönen. Wegen dieser Unsymmetrie deckt die Tonleiter nur die Harmonien ausgehend vom Grundton c ab. Bei einem anderen Grundton fehlen manche der wohlklingenden Frequenzverhältnisse. Um die Lücken zu schließen, werden neue Töne eingefügt, die entweder[1]
| Bezeichnung der neuen Töne | |
|---|---|
| cis, dis, fis, gis, ais |
| des, es, ges, as, b |
Ideale und gleichstufige Tonleiter auf der Cent-
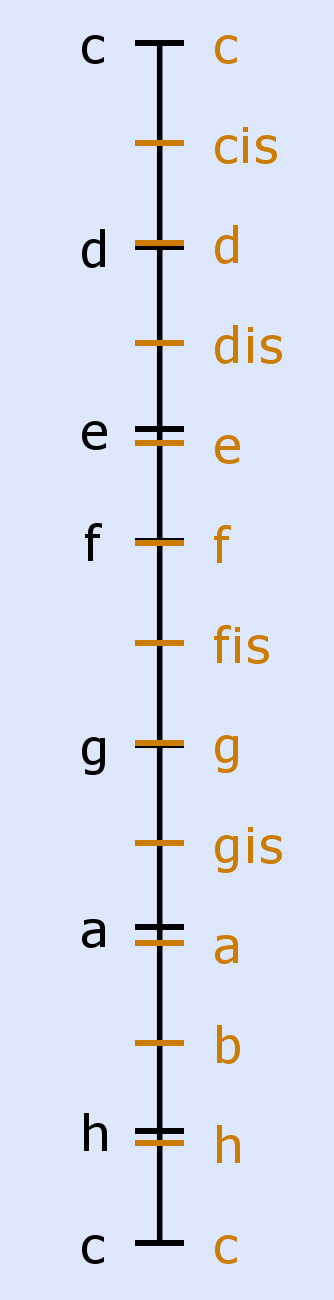
Auch andere Verhältnisse als 1/24 sind möglich und üblich. Allerdings wird in jedem Fall die Tonleiter mit einem anderen Grundton als c die Harmonien nur näherungsweise wiedergeben, da die für c exakten Frequenzverhältnisse für andere Grundtöne nicht exakt stimmen. Daher klingt auf einem so gestimmten Instrument nicht jede Tonleiter gleich.
Gleichstufige Tonleiter
Tatsächlich werden (heutzutage) die zwölf Töne der Tonleiter einfach zwischen Grundton und Oktave (= Ton mit doppelter Frequenz) gleichmäßig verteilt: Jeder Ton hat dasselbe Verhältnis zum nächsten, nämlich 1,05946... (= 12. Wurzel von 2, also 1,05946...12 = 2), d. h. jeder Ton hat eine um 5,946...% höhere Frequenz als der vorige (= 100 Cent mehr).
| Abk. | Frequenz | |||||
|---|---|---|---|---|---|---|
| exakt | gleichstufig | Differenz | ||||
| c | Grundton | = 0 Cent | Grundton | = 0 Cent | 0 | 0 Cent |
| cis | 1,04167·Grundton | ≈ 71 Cent | 1,05946·Grundton | = 100 Cent | +0,01780 | +29 Cent |
| des | 1,08000·Grundton | ≈ 133 Cent | −0,02054 | −33 Cent | ||
| d | 1,12500·Grundton | ≈ 204 Cent | 1,12246·Grundton | = 200 Cent | −0,00254 | −4 Cent |
| dis | 1,17188·Grundton | ≈ 275 Cent | 1,18921·Grundton | = 300 Cent | +0,01733 | +25 Cent |
| es | 1,20000·Grundton | ≈ 316 Cent | −0,01079 | −16 Cent | ||
| e | 1,25000·Grundton | ≈ 386 Cent | 1,25992·Grundton | = 400 Cent | +0,00992 | +14 Cent |
| f | 1,33333·Grundton | ≈ 498 Cent | 1,33484·Grundton | = 500 Cent | +0,00151 | +2 Cent |
| fis | 1,38889·Grundton | ≈ 569 Cent | 1,41421·Grundton | = 600 Cent | +0,02532 | +31 Cent |
| ges | 1,44000·Grundton | ≈ 631 Cent | −0,02579 | −31 Cent | ||
| g | 1,50000·Grundton | ≈ 702 Cent | 1,49831·Grundton | = 700 Cent | −0,00169 | −2 Cent |
| gis | 1,56250·Grundton | ≈ 773 Cent | 1,58740·Grundton | = 800 Cent | +0,02490 | +27 Cent |
| as | 1,60000·Grundton | ≈ 814 Cent | −0,01260 | −14 Cent | ||
| a | 1,66667·Grundton | ≈ 884 Cent | 1,68179·Grundton | = 900 Cent | +0,01513 | +16 Cent |
| ais | 1,73611·Grundton | ≈ 955 Cent | 1,78180·Grundton | = 1000 Cent | +0,04569 | +45 Cent |
| b | 1,80000·Grundton | ≈ 1018 Cent | −0,01820 | −18 Cent | ||
| h | 1,87500·Grundton | ≈ 1088 Cent | 1,88775·Grundton | = 1100 Cent | +0,01275 | +12 Cent |
| c | 2,00000·Grundton | = 1200 Cent | 2,00000·Grundton | = 1200 Cent | 0 | 0 Cent |
Mit dieser gleichstufigen Stimmung ist jede Tonleiter gleich gut spielbar. Die Abweichungen zu den idealen Frequenzverhältnissen sind aber durchaus hörbar. Sie werden notgedrungen in Kauf genommen. Man hat sich daran gewöhnt, sie nicht mehr zu hören.[2]
Vergangenheit
Ursprünglich lautete die Tonleiter einfach a, b, c, d, e, f, g. Das b spaltete sich im 10. Jahrhundert in einen tieferen und einen höheren Ton. Der höhere wurde h genannt; das b weggelassen.[3] Später wurde es allmählich gebräuchlich, die Tonleiter mit c statt a zu beginnen.[4]
Jahrhundertelang wurde getüftelt, wie man die Tonleiter am besten auf’s Klavier bringt. Erst im 19. Jahrhundert[5] setzte sich die Erkenntnis durch, dass die gleichmäßige Stimmung der beste Kompromiss ist. Bei elektronisch erzeugter Musik könnten die exakten Frequenzverhältnisse genommen werden. Ich habe bisher aber noch nicht gelesen, dass das gemacht wird (nur für alte Musik[6]).
Weiter
Weblinks
- Wikipedia: Vergleich der Stimmungssysteme
Quellen
| [1] | Die Physik. Ein Lexikon der gesamten Schulphysik. Mannheim: Bibliographisches Institut/Dudenverlag, 1974, S. 413f. |
| [2] | Die Musik. Ein Sachlexikon der Musik. Mannheim: Bibliographisches Institut, 1979, S. 383 |
| [3] | Wieland Ziegenrücker: Allgemeine Musiklehre. mit Fragen und Aufgaben zur Selbstkontrolle. München: Goldmann, 7. Aufl. 1984 (Original 1977), S. 19 |
| [4] | Werner Neumann (Hrsg.): Katechismus der Musik. Als Neubearbeitung und Erweiterung des gleichnamigen Werkes von J. C. Lobe. Wiesbaden: Breitkopf & Härtel, 1975 (1.? Aufl. 1950), S. 4 |
| [5] | Walter Knapp, Wolf Peschl: Wege zur Musik. AHS- |
| [6] | Schulbuch Musik in Europa. 1. Teil: Die theoretischen Grundlagen (Reihe: Wir lernen Musik, 5. Band), Wien: Ludwig Doblinger, 1963, S. 23 – „Auch heute noch musizieren gute A-cappella- |
