Falsche Anwendung der Bernoulli-Gleichung
Im Internet, im Fernsehen und sogar in Schulbüchern sowie wissenschaftlichen Zeitschriften[1] werden sehr häufig Effekte mit der Bernoulli-
| Effekt | Falsche Erklärung | Richtige Erklärung | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Die sich bewegende Luft übt einen geringeren Druck aus. Der Umgebungsdruck ist höher und drückt das Papier in den Luftstrom.[2] |
Wenn die Luft aus dem Mund austritt, nimmt sie sehr rasch den Umgebungsluftdruck an.[3] (Entweder sie dehnt sich aus oder sie wird vom Umgebungsdruck zusammengedrückt.) Der beobachtete Auftrieb liegt an der gekrümmten Oberfläche des so gehaltenen Papiers. Die Luft wird quasi vom Papier angezogen (Coanda- Liegt das Papier flach am Tisch, kann kein Auftrieb erzielt werden. Auch wenn das Papier gerade nach unten hängt und auf einer Seite von oben angeblasen wird, passiert nichts Besonderes. | 
| |||||||||||||||||
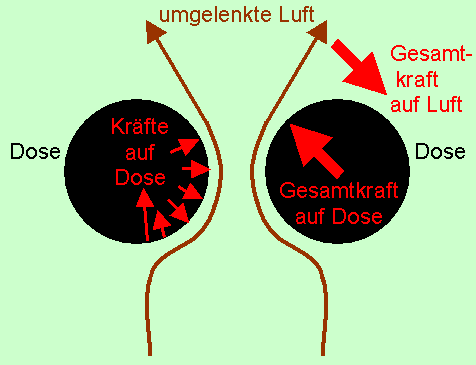
Zwischen den Dosen bewegt sich die Luft besonders schnell. Daher sinkt laut Bernoulli-|
| Die Luft wird von der Rückseite jeder Dose "angezogen" (Coanda- Bringt man einen Karton auf der Rückseite der Dosen an, der das Um- Vor den Dosen kann sich die Luft ein wenig stauen, sodass der Druck zwischen ihnen laut Bernoulli-
Mit Karton wird keine Luft umgelenkt und daher entsteht keine Anziehungskraft mehr.
| Im Luftstrom ist der Druck geringer als außerhalb. Gelangt der Ball an die Grenze des Luftstroms, wird er daher vom äußeren Luftdruck wieder hineingedrückt.
| Im Luftstrom ist der Druck nicht geringer als außerhalb.[5] Das kann leicht gemessen werden. Tatsächlich wird die strömende Luft von dem Ball "angezogen" (Coanda- | ähnlich wie bei einer Dose (siehe oben)
|
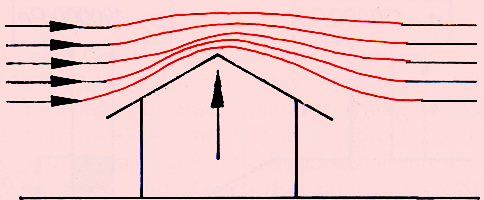
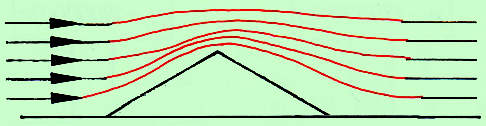
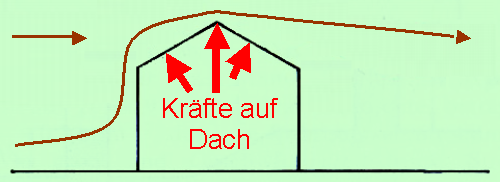
| Das Dach verengt den Querschnitt, der dem Wind zur Verfügung steht. Folglich muss über dem Dach die Geschwindigkeit zunehmen. Strömt Luft sehr schnell gegen ein Dach, so ist die Strömungsgeschwindigkeit auf der Seite des Daches besonders groß, die in Richtung der strömenden Luft liegt. Demzufolge ist dort der statische Druck (d. h. der Druck quer zur Strömungsrichtung, also in Richtung Dach) relativ klein.
|
(Aus einem Schulbuch[6])
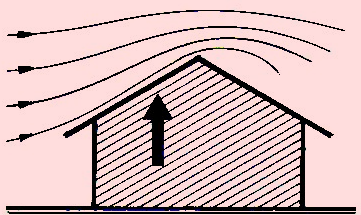
(Anderes Schulbuch[7])
| Wenn der Wind so wie gezeichnet bläst, dann wird er auf der angeblasenen Seite des Daches nach oben abgelenkt; auf das Dach wirkt daher eine Kraft nach unten. Über der Dachspitze und auf der windabgewandten Seite ist es umgekehrt: Der Wind wird vom Dach "angezogen" (Coanda- In der Praxis ist die Situation aber komplizierter: 1. Der Wind bläst auch gegen die senkrechte Wand und wird dort nach oben abgelenkt. Wenn er das Dach erreicht, kann er trotz "Kollision" mit der horizontalen Anströmung eine Richtung, die vom Dach wegzeigt, haben. In dem Fall wird er daher vom Dach angezogen (Coanda- 2. An Überhängen oder Vorsprüngen kann sich der Wind zusätzlich "fangen" und hohen Druck produzieren.[9]
|
Nur wenn das Dach direkt am Boden stünde, würde der Wind annähernd so wie gezeichnet strömen. Die rechte Seite stimmt auch dann nicht, weil der Wind so einer scharfen Ecke nicht wirklich folgen kann. Es entstehen stattdessen Turbulenzen.
Mit Hauswand ist die Stromlinie des Windes zum Dach gekrümmt. Daher wirkt der Sog, der den Coanda-
Wind kann sich am Vorsprung "fangen".
| Über dem Regenschirm ist der Staudruck (Druck in Strömungsrichtung) wegen der höheren Geschwindigkeit größer als davor oder dahinter – und damit ist laut Bernoulli- |
| Die Windgeschwindigkeit über dem Regenschirm muss tatsächlich größer sein, aber auf den Regenschirm wirkt nicht nur der statische Druck, sondern wegen der Umlenkung des Windes auch ein Anteil Staudruck bzw. "Coanda- Auf der windzugewandten Seite kann in Summe kein Auftrieb entstehen, weil die Luft nach Passieren der ganzen Vorderseite bestenfalls wieder waagrecht strömt. Erst wenn der Wind auch der abgewandten Seite folgt und er am Ende zumindest ein bisschen Richtung Erdboden strömt, kann auf den Regenschirm eine entsprechende Gegenkraft nach oben wirken. In der Praxis kommt der Wind nicht immer genau von vorne. Gelangt eine Böe von unten in den Schirm, kann dieser leicht umgedreht werden, ohne dass das irgendetwas mit der Bernoulli- Testet man Schirme im Windkanal, dann heben manche tatsächlich irgendwann ab.[10] Viele Schirme scheinen allerdings eher kaputtzugehen als umzuklappen,[11] evtl. weil sie von Sturm so verformt werden, dass die Luft keinen schönen Bogen mehr hat, an dem sie entlangströmen und Auftrieb erzeugen könnte. Stabilere Schirme neigen sich ein wenig in die Richtung, aus der der Wind bläst.[12] Das liegt daran, dass die Luft zuerst nach oben abgelenkt wird, dann später wieder nach unten. Entsprechend wirkt auf den ersten Abschnitt des Schirms eine Kraft nach unten und auf den restlichen Teil eine nach oben, insgesamt also ein Drehmoment. Der gleichmäßige Luftstrom im Windkanal scheint aber die meisten Schirme nicht zum Umklappen zu bringen. 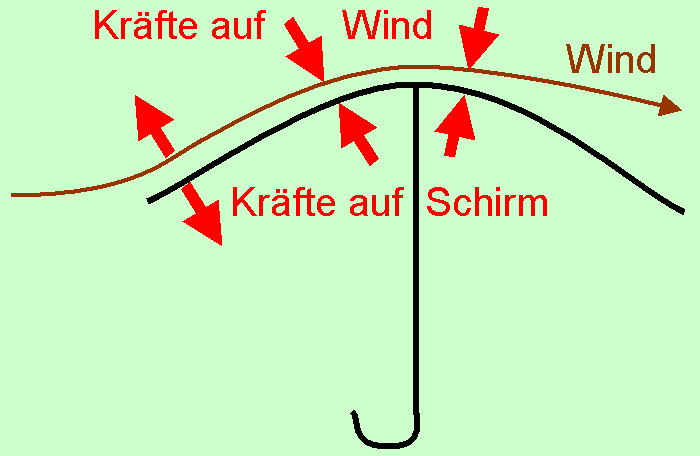
| Die schnell ausgeatmete Luft hat einen geringeren Druck und daher wird zusätzliche Luft aus der Umgebung angesaugt.
|
| Die schnell ausgeatmete Luft zieht Luft der Umgebung aufgrund der Reibung zwischen Luftschichten (Viskosität) mit. Es wird zwar tatsächlich die Luft unmittelbar nach dem Ausatmen einen leichten Unterdruck haben, so wie die Bernoulli-
| | |||
Zusammenfassung
Die falschen Anwendungen der Bernoulli-
- Hohe Geschwindigkeit wird mit geringem Druck gleichgesetzt (Übervereinfachung der Bernoulli-
Gleichung, die auf frei strömende Luft so angewandt wird, als würde sie in Rohren fließen). - Der Effekt von gekrümmten Oberflächen, an denen die Luft entlangströmt, wird vernachlässigt.[13]
Mein Fazit
Es ist erstaunlich, wie gut das Bernoulli-
Kein Wunder, dass viele Leute das Gefühl haben, die Bernoulli-
Zur richtigen Deutung der Phänomene in freier Strömung helfen meist die Newton'schen Gesetze:
- Jede Bewegungsänderung erfordert eine Kraft.
- Zu jeder Kraft gibt es eine gleich große Gegenkraft.
Weiter
Weblinks
- Englische Wikipedia: Misapplications of Bernoulli's principle in common classroom demonstrations
- Hydrodynamic Levitation! (Video, englisch) – Ball schwebt in Wasserstrahl (Springbrunnen), nicht wegen Bernoulli-
Effekt, sondern ähnlich wie Ping- Pong- Ball im Fön, nur dass hier Wasser und nicht Luft um die Ecke gezogen und abgelenkt wird.
Quellen
| [1] | Peter Eastwell: Bernoulli? Perhaps, but What About Viscosity? (PDF), S. 2 | ||||||||||||||
| [2] |
| ||||||||||||||
| [3] |
| ||||||||||||||
| [4] | Fermilab: The Newtonian Description of Lift of a Wing (PDF), S. 12 | ||||||||||||||
| [5] | Fermilab: The Newtonian Description of Lift of a Wing (PDF), S. 11f. | ||||||||||||||
| [6] | Karl Hammer, Peter Svoboda, Lutz Trieb: Physik, Band 1: Mechanik, Wärmelehre, Optik, Wien: R. Oldenbourg Verlag, 2. Auflage 1989, S. 97 | ||||||||||||||
| [7] | Josef Schreiner: Angewandte Physik, Teil 1: Mechanik, Thermodynamik, Optik, Wien: ÖBV & HPT, 1. Auflage 2001 (ISBN 3-209-| [8]
| CFD Prediction on the Pressure Distribution and Streamlines around an Isolated Single- | [9]
| Peter Eastwell: Bernoulli? Perhaps, but What About Viscosity? (PDF), S. 11
| [10]
| Awnet 2m Umbrella with Weight Bags Wind Tunnel Test (Video)
| [11]
| Ausbrella v Awnet v Imported Umbrella Wind Tunnel Comparison 2013 (Video)
| [12]
|
| [13]
| Klaus Weltner: Misinterpretations of Bernoulli's Law (PDF), S. 5 – "As a rule, physics textbooks neglect the treatment of normal acceleration of fluids in curved streamlines. The neglect of pressure gradients related to curved streamlines is disastrous because the mechanism producing low pressure in streaming fluids is thus made impossible to be understood."
| [14]
|
|
|