Bernoulli-Gleichung auf Mikroebene

Ich habe lange darüber nachgedacht, wie zu verstehen ist, dass eine "Bernoulli'sche" Strömung vor einer Engstelle beschleunigt. Woher "wissen" die einzelnen Atome oder Moleküle, dass sie schneller werden sollen? Dass es aufgrund der Energieerhaltung so sein muss, war mir rasch klar, aber der tieferliegende Grund blieb im Dunkeln. (So geht es auch vielen Studenten und Lehrern.^[1])

Kein einziges Physik-Buch, das ich zu Rate zog, verlor darüber auch nur ein Wort. Sogar der berühmte Physiker Richard Feynman begnügte sich voll und ganz mit der Herleitung aufgrund der Energieerhaltung.^[2]

Im Internet habe ich vereinzelt die von mir gewünschten Erklärungen gefunden, die sich jedoch als falsch erwiesen:

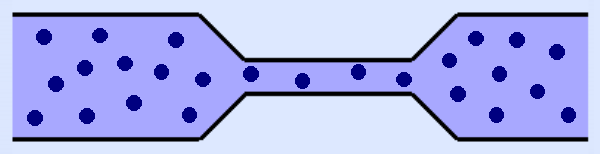
Auf Mikroebene gibt es kein kontinuierliches Medium, sondern einzelne Teilchen, die sich in alle Richtungen bewegen.

Hydrodynamisches Paradoxon: Obwohl die Luft voll auf ein Hindernis prallt, wird dieses nicht weggeblasen, sondern sogar angezogen. – Normalerweise reagiert ein System so, dass es einem Zwang möglichst ausweicht. In dem Fall ist das aber nicht möglich, weil beim Ausströmen der Druck sinkt.

Erklärung	Gegenargumente
Moleküle bewegen sich aufgrund ihrer Wärmeenergie in alle Richtungen. Moleküle, die in eine Engstelle gelangen, sind mit größerer Wahrscheinlichkeit solche, die sich in Strömungsrichtung als quer dazu bewegen. Deswegen prallen sie seltener auf die Rohrwand und in einem flacheren Winkel, d. h. sie üben weniger Kraft auf die Rohrwand aus. Sie benutzen einen Teil ihrer Wärmebewegung, um insgesamt schneller durch das enge Rohr zu fließen. Der Eingang zur Engstelle wirkt wie ein Filter, der nur Moleküle mit einer gewissen Flugrichtung und Geschwindigkeit durchlässt.	Meine erste Annahme war auch, dass die Teilchen im schnellen Strom irgendwie "zu beschäftigt" sind, um quer zu ihrer raschen Bewegung noch viel Druck auszuüben. Aber es passt nicht:^[3] Die Teilchen kollidieren ca. alle 10–100 nm miteinander. Selbst wenn ursprünglich alle nahezu exakt waagrecht flogen, wird das nicht lange so bleiben. Es wäre zu erwarten, dass die Bernoulli-Gleichung für längere Rohrstücke nicht mehr gilt. Es wäre auch schwer zu verstehen, wie die "gefilterte" Geschwindigkeit in gebogenen Rohrstücken aufrecht erhalten bleibt. Die Bernoulli-Gleichung gilt sogar dann, wenn die Teilchen nach der Öffnung sofort in alle Richtungen umgeleitet werden. (Versuch zum hydrodynamischen Paradoxon) Ein Geschwindigkeitsfilter-Effekt erscheint bei einem kleinen Loch plausibel. Die Bernoulli-Gleichung gilt aber auch dann, wenn sich der Querschnitt ganz sanft und/oder nur geringfügig ändert. Ich habe auch überlegt, ob vielleicht einfach Wärmebewegung in geordnete Geschwindigkeit umgewandelt wird. Aber eine Geschwindigkeitszunahme um 10 m/s kann mit einem Druckabfall auf die Hälfte verbunden sein, obwohl sich die Teilchen auf Mikroebene mit ca. 500 m/s bewegen. Es wäre in der Betrachtung nur eine Druckänderung in der Größenordnung von ¹⁰/₅₀₀ = ¹/₅₀ zu erwarten.
Wenn auf einer Straße ein Auto pro Sekunde fährt, dann hängt der Abstand zwischen zwei Autos von deren Geschwindigkeit ab: Fahren sie alle mit 1 m/s, dann ist der Abstand 1 m. Fahren sie mit 10 m/s, dann ist der Abstand 10 m. Genauso ist es mit den Molekülen in einer "Bernoulli'schen" Strömung. Und wenn der Abstand steigt, dann sinkt der Druck – schlicht weil weniger Teilchen da sind, die "drücken" können.	In einem Rohr fließt durch jeden Querschnitt dieselbe Menge pro Zeit. Der dünne Querschnitt hat weniger Fläche, die genau die größere Geschwindigkeit kompensiert, sodass der Abstand zwischen den Molekülen nicht zunehmen muss. Es wäre auch rätselhaft, wieso Wassermoleküle, die unter hohem Druck stehen, extra großen Abstand halten, wenn sie durch die Engstelle rasen.

Erklärung

Gegenargumente

Moleküle bewegen sich aufgrund ihrer Wärmeenergie in alle Richtungen. Moleküle, die in eine Engstelle gelangen, sind mit größerer Wahrscheinlichkeit solche, die sich in Strömungsrichtung als quer dazu bewegen. Deswegen prallen sie seltener auf die Rohrwand und in einem flacheren Winkel, d. h. sie üben weniger Kraft auf die Rohrwand aus. Sie benutzen einen Teil ihrer Wärmebewegung, um insgesamt schneller durch das enge Rohr zu fließen. Der Eingang zur Engstelle wirkt wie ein Filter, der nur Moleküle mit einer gewissen Flugrichtung und Geschwindigkeit durchlässt.

Meine erste Annahme war auch, dass die Teilchen im schnellen Strom irgendwie "zu beschäftigt" sind, um quer zu ihrer raschen Bewegung noch viel Druck auszuüben. Aber es passt nicht:^[3]

Die Teilchen kollidieren ca. alle 10–100 nm miteinander. Selbst wenn ursprünglich alle nahezu exakt waagrecht flogen, wird das nicht lange so bleiben. Es wäre zu erwarten, dass die Bernoulli-Gleichung für längere Rohrstücke nicht mehr gilt.
Es wäre auch schwer zu verstehen, wie die "gefilterte" Geschwindigkeit in gebogenen Rohrstücken aufrecht erhalten bleibt. Die Bernoulli-Gleichung gilt sogar dann, wenn die Teilchen nach der Öffnung sofort in alle Richtungen umgeleitet werden. (Versuch zum hydrodynamischen Paradoxon)
Ein Geschwindigkeitsfilter-Effekt erscheint bei einem kleinen Loch plausibel. Die Bernoulli-Gleichung gilt aber auch dann, wenn sich der Querschnitt ganz sanft und/oder nur geringfügig ändert.
Ich habe auch überlegt, ob vielleicht einfach Wärmebewegung in geordnete Geschwindigkeit umgewandelt wird. Aber eine Geschwindigkeitszunahme um 10 m/s kann mit einem Druckabfall auf die Hälfte verbunden sein, obwohl sich die Teilchen auf Mikroebene mit ca. 500 m/s bewegen. Es wäre in der Betrachtung nur eine Druckänderung in der Größenordnung von ¹⁰/₅₀₀ = ¹/₅₀ zu erwarten.

Wenn auf einer Straße ein Auto pro Sekunde fährt, dann hängt der Abstand zwischen zwei Autos von deren Geschwindigkeit ab:
- Fahren sie alle mit 1 m/s, dann ist der Abstand 1 m.
- Fahren sie mit 10 m/s, dann ist der Abstand 10 m.
Genauso ist es mit den Molekülen in einer "Bernoulli'schen" Strömung. Und wenn der Abstand steigt, dann sinkt der Druck – schlicht weil weniger Teilchen da sind, die "drücken" können.

In einem Rohr fließt durch jeden Querschnitt dieselbe Menge pro Zeit. Der dünne Querschnitt hat weniger Fläche, die genau die größere Geschwindigkeit kompensiert, sodass der Abstand zwischen den Molekülen nicht zunehmen muss. Es wäre auch rätselhaft, wieso Wassermoleküle, die unter hohem Druck stehen, extra großen Abstand halten, wenn sie durch die Engstelle rasen.

Bei Luft stimmt es, dass in der schnelleren Strömung der Abstand der Teilchen untereinander steigt:

Bei Gasen wie Luft ist der Druck mehr oder weniger proportional zur Dichte. Höherer Druck heißt: mehr Teilchen prallen auf dieselbe Fläche (in der gleichen Zeit).
Bei Flüssigkeiten wie Wasser ändert sich die Dichte kaum mit dem Druck. Die Wassermoleküle stoßen sich stark ab, wenn sie auch nur ein bisschen näher gebracht werden. Höherer Druck ergibt sich bei ihnen nicht durch mehr Teilchen, sondern aus dieser höheren Abstoßungskraft, die die Wassermoleküle auch auf die Wand ausüben.

Dieses unterschiedliche Verhalten lässt sich schwer zu einem anschaulichen Bild von "dem" Bernoulli-Effekt vereinen.

Mein Fazit

Die Bernoulli-Gleichung kann nicht auf der Mikroebene veranschaulicht werden. Alles, was man zu ihrem Verständnis wissen muss, ist in den makroskopischen Größen wie Druck und Geschwindigkeit enthalten.

Was schon stimmt

Bei idealen Gasen kann der Geschwindigkeitsgewinn in der Engstelle nur aus der Wärmebewegung kommen. (Es gibt kein Kraftfeld, das die Teilchen beschleunigen könnte und zwischen idealen Gasteilchen wirken auch keine Kräfte.) Daraus folgt:

Das schnell strömende Gas ist kühler als das langsam strömende (gemessen mit mitbewegtem Thermometer).
Es gibt für Gase eine Obergrenze für die erreichbare Geschwindigkeit, nämlich die Geschwindigkeit, die die kleinsten Teilchen haben. Das ist in etwa die Schallgeschwindigkeit. (In diesen Bereichen gilt die Bernoulli-Gleichung aber schon deshalb nicht mehr, weil das Medium dann nicht mehr als inkompressibel angenommen werden kann.)

Weiter

Falsche Anwendung der Bernoulli-Gleichung

Quellen

[1]	Klaus Weltner: Misinterpretations of Bernoulli's Law (PDF), S. 1 – "Students and Instructors are often left with an uncomfortable feeling that the equation is clear and its predictions are verified, but the real underlying cause of the predicted pressure changes is obscure." Paul G. Hewitt: Bernoulli's Principle – "Several physics teachers I've recently spoken with say their understanding of Bernoulli's principle is unclear, particularly when the principle is applied to aerodynamic lift."
[2]	Richard P. Feynman, Robert B. Leighton, Matthew Sands: Vorlesungen über Physik. Band 2: Hauptsächlich Elektromagnetismus und Struktur der Materie. München: Oldenburg, 1987 (amerik. Original 1963), S. 814
[3]	Peter Eastwell: Bernoulli? Perhaps, but What About Viscosity? (PDF), S. 4 – "One finds the argument that, when air is caused to move in one direction, the particles are somehow so occupied with moving in that direction that they now no longer have time to push as hard laterally (e.g., Niven, 1999). This idea might be intuitive to some, but it has no basis in science."

Seite erstellt am 10.11.2019 – letzte Änderung am 17.11.2019

Wissenschaft

Hauptthemen

Bernoulli-Gleichung auf Mikroebene

Mein Fazit

Was schon stimmt

Weiter

Quellen