Siehe auch
HauptthemenBernoulli-Gleichung
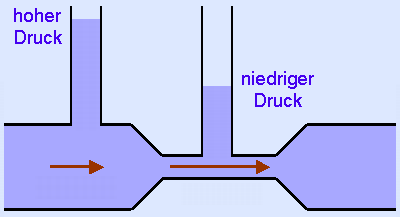
Wenn eine Flüssigkeit oder ein Gas durch eine Engstelle muss, dann staut sie sich vor ihr so lange, bis pro Zeiteinheit genauso viel zufließt wie abfließt. Die Geschwindigkeit im engen Stück wird höher sein.
Das ist leicht einzusehen, aber im engen Stück sinkt auch der Druck.
Bernoulli-
p + ρv2/2 = konstant
| p | = | Druck |
| ρ | = | Masse pro Volumen (Dichte) |
| v | = | Geschwindigkeit |
Wieso? Weil die Energieerhaltung gilt:
potenzielle Energie + kinetische Energie = konstant
Druck ist potenzielle Energie, Geschwindigkeit entspricht kinetischer Energie. Wenn die Geschwindigkeit steigt, muss daher der Druck sinken. Das ist die Hauptaussage der Bernoulli-
Plausibilisierung:
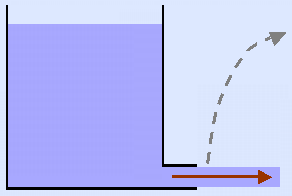
Die Bernoulli-
Maximale Geschwindigkeitsdifferenz in Luft und in Wasser
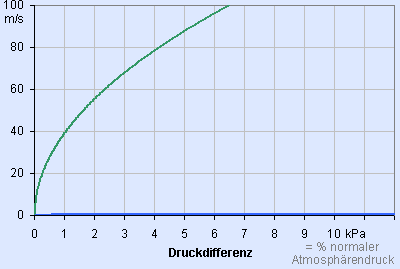
Zusammenhang von Druck und Geschwindigkeit laut Bernoulli-
Voraussetzungen
- Die Gleichung gilt so nur für Strömungen in Rohren![2] Wenn es keine Wand gibt, dann kann sich der Druck an die Umgebung anpassen.[3] Viele Beispiele für falsche Anwendung der Bernoulli-
Gleichung beruhen auf Missachtung dieser Voraussetzung. Eine Wand ist nur dann nicht erforderlich, wenn die Strömung durch ein passives Hindernis umgelenkt wird: Dann kommt es lokal zu Druck- und Geschwindigkeitsänderungen, die der Bernoulli-Gleichung gehorchen. - Es darf keine Energie von außen zugeführt werden. Z. B. bei einer Pumpe gilt die Bernoulli-
Gleichung nicht. Auch nicht, wenn das Medium erhitzt wird - Es darf keine Energie abgegeben werden. Das wäre der Fall, wenn es Reibung gibt. Reibung entspricht Energieverlust. In der Realität gibt es immer Reibung, daher gilt die Bernoulli-
Gleichung in der Praxis immer nur näherungsweise. - Das Medium darf nicht komprimierbar sein. Ansonsten ist die Dichte in der Bernoulli-
Gleichung keine Konstante und es müssten u. U. weitere Energieformen berücksichtigt werden. Z. B. wenn unter Druck stehendes Gas expandiert, kühlt es ab. In Wirklichkeit ist jedes Medium komprimierbar. Flüssigkeiten nur so wenig, dass der Effekt vernachlässigbar klein ist; Gase stark, aber bis zu Geschwindigkeitsänderungen um ca. 30% der Schallgeschwindigkeit ist der Fehler dennoch kleiner als 5%. Deswegen wird die Bernoulli- Gleichung erfolgreich auch auf Luft angewandt. - Die Strömung darf sich nicht ändern. Sie muss insbesondere frei von Turbulenzen sein. Nur dann kann man den Energieerhaltungssatz auf verschiedene Abschnitte der Rohre anwenden.
Wie immer in der Physik sind die Voraussetzungen nicht als strikte Verbote zu verstehen. Die Gleichung wird nicht sofort komplett falsch, wenn Bedingungen nicht ganz erfüllt sind. Wichtig ist allerdings, zu wissen, unter welchen Umständen der Fehler klein bleibt.
Verallgemeinerung
Bernoulli-
p + ρv2/2 + ρgh = konstant
| g | = | Erdbeschleunigung = 9,81 m/s2 |
| h | = | Höhe (gemessen von einem beliebigen, aber festen Punkt) |
- Die Bernoulli-
Gleichung gilt auch, wenn das strömende Medium im Rohr auf verschiedenen (aber konstanten) Bahnen fließt, u. U. mit verschiedener Geschwindigkeit. Die Bernoulli- Gleichung gilt dann entlang von Stromlinien (die wegen der konstanten Strömung gleichzeitig Bahnlinien sind). Voraussetzung ist allerdings weiterhin, dass entlang der ganzen Stromlinie keine Energie zugeführt oder abgeführt wird. Wenn sich z. B. zwei Strahlen kreuzen oder wenn ein Strahl vom Umgebungsdruck zusammengepresst wird, dann ist die Voraussetzung nicht erfüllt. - Zur potenziellen Energie kann die Lageenergie im Gravitationsfeld als eigener Term hinzugefügt werden.
- Weitere Energieformen und Komprimierbarkeit können in komplizierteren Gleichungen abgebildet werden.
Missverständnisse
Das Bernoulli-Prinzip ist leicht zu verstehen, wenn es richtig formuliert wird. Wir müssen jedoch aufpassen, denn scheinbar kleine Änderungen in der Wortwahl können zu falschen Schlussfolgerungen führen.
Frei fließende Flüsse nehmen alle den Atmosphärendruck an.
Vor einer Engstelle muss der Wasserspiegel etwas höher sein, damit das Wasser beschleunigt werden kann. Bei Eintritt in die Engstelle fällt der Druck laut Bernoulli-
In Turbinen kann der Druck fast auf 0 abfallen (mit Gefahr von Beschädigung).
- Es ist keineswegs so, dass in einem schnell fließenden Fluss ein geringerer Druck als in einem langsam fließenden herrscht. Auch wenn sich Luft bewegt, muss nicht unbedingt der Druck abfallen.
- Zuerst muss ein Druckunterschied da sein, dann kann daraus eine Geschwindigkeitsänderung entstehen – nicht umgekehrt.[4]
- Druckunterschiede entstehen
- wenn sich das Medium vor einer Engstelle oder einem Hindernis staut
- wenn das Medium umgelenkt wird (d. h. quer zur Bewegungsrichtung beschleunigt wird), z. B. in gebogenen Rohren oder wenn das Medium einer gekrümmten Oberfläche folgt (Coanda-
Effekt ).
- Es ist falsch, dass das Medium an der Engstelle schneller fließen "muss". Richtig ist, dass die Bedingung erfüllt sein muss, damit die Strömung zeitlich unveränderlich ist und somit Bernoullis Gleichung angewandt werden kann. Passen Druck und Geschwindigkeiten nicht zusammen, werden sich Druck und Geschwindigkeit so lange ändern, bis ein Gleichgewicht erreicht ist.
Anwendungen
- Mit Druckluft saugen – Habe ich in der HTL in der Werkstätte gesehen.
- Treibstoffvergaser
Theorie
- Flugzeugflügel – Mit der Bernoulli-
Gleichung kann man Druck und Geschwindigkeit näherungsweise ineinander umrechnen. Die Bernoulli- Gleichung erklärt jedoch nicht, wie es zu der beobachteten Druckverteilung am Flugzeugflügel kommt. - Kavitation – Wenn Druck rasch abgebaut wird, kann (kurzzeitig) so starker Unterdruck entstehen, dass Material beschädigt wird.
Bezeichnungen
- Mit "Druck" meine ich den Druck quer zur Strömungsrichtung. Dieser entspricht auch dem Druck, den ein mit der Strömung mitbewegtes Manometer anzeigt. Dieser Druck wird von Fachleuten "statischer Druck" genannt.
- Frontal zur Strömung ist der Druck höher – logisch, weil sich das Medium staut und mit seiner Trägheit eine Extra-
Kraft ausübt. Dieser Druck heißt "Staudruck", "dynamischer Druck" oder "Geschwindigkeitsdruck". Er kann z. B. gefühlt werden, wenn man mit einem Gartenschlauch angespritzt wird.
Weiter
Quellen
| [1] |
|
| [2] |
|
| [3] | David F. Anderson, Scott Eberhardt: The Newtonian Description of Lift of a Wing (PDF), S. 11f. – "At the exit from the hairdryer or from your lips the stream of air adjusts itself by expanding or contracting to have the same value of ps as the surrounding air." |
| [4] | Jörn Loviscach: Drei Überraschungen beim Satz von Bernoulli (Video), ab 7:47 |